VELOCIDAD LINEAL
Representación Gráfica de la velocidad angular
La velocidad angular, al igual que la velocidad lineal es una magnitud vectorial, la cual se representa mediante un vector que es perpendicular al plano de la circunferencia que describe la partícula. Su sentido es el mismo de avance de un tirabuzón, cuando gira en el mismo sentido que tiene el móvil o la partícula.
Ecuación de la velocidad angular en
función de la frecuencia. La ecuación de la velocidad angular en función del periodo es:
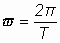
pero
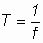
Luego:
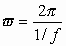
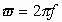 Ecuación de la velocidad lineal en función de la frecuencia.
Ecuación de la velocidad lineal en función de la frecuencia.
La ecuación de la velocidad lineal en función del periodo es:

luego,
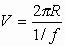
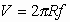 Relación entre la velocidad lineal y la velocidad angular
Relación entre la velocidad lineal y la velocidad angular
Las
ecuaciones de la velocidad lineal y velocidad angular vienes dadas por:
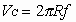 .................................................. ..................................................
| (1)
|
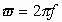 ..................................................... .....................................................
| (2)
|
Cuando se estudió la aceleración en el
movimiento rectilíneo, dijimos que ella no era más que el
cambio constante que experimentaba la velocidad por unidad de
tiempo. La velocidad cambiaba únicamente en
valor numérico, no así en
dirección.
Cuando el móvil o la partícula realiza un movimiento circular uniforme, es lógico pensar que en cada punto el valor numérico de la velocidad es el mismo, en cambio es fácil darse cuenta que la dirección de la velocidad va cambiando a cada instante. La variación de dirección del vector lineal origina una aceleración que llamaremos
aceleración centrípeta. Esta aceleración tiene la dirección del
radio apuntando siempre hacia el centro de la circunferencia, razón por la cual también se llama
Aceleración Radial. Las direcciones de la velocidad tangencial y de la aceleración centrípeta, son perpendiculares
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Ecuación de la Aceleración Centrípeta:
Para ver el gráfico seleccione la opción "Descargar" del menú superior
En el punto A de su trayectoria tiene una velocidad V1 y en un intervalo de tiempo D t ocupa el punto B con velocidad V2. Aquí las dos velocidades difieren únicamente en dirección, pues sus magnitudes son iguales.
Por otra parte sabemos que la velocidad instantánea y la aceleración vienen dadas respectivamente por:
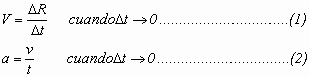
Vectorialmente, el cambio de velocidad se obtiene haciendo la diferencia V=V2 - V1, donde se cambia el sentido del vector V1 y se hace la suma vectorial.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
La velocidad angular es la magnitud medida por el cociente entre el ángulo descrito por el radio vector y el tiempo empleado en describirlo.
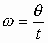
w se mide en rad/s.
Cuando el ángulo barrido es un ángulo de giro igual a 2P , el tiempo empleado es un período, pudiéndose escribir que:
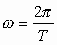
La velocidad angular es el ángulo recorrido en la unidad de tiempo. Sea
w este ángulo. Si un móvil animado de movimiento circular describe el arco MOM= a en un tiempo t, la velocidad angular
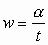
siendo R el radio de la trayectoria circular y
v la velocidad lineal, se demuestra que:
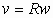
y se expresa
w en radianes.
- DINÁMICA DEL MOVIMIENTO CIRCULAR UNIFORME
La
fuerza que resulta de este movimiento entonces también debe apuntar hacia el centro. No hay que olvidar que esta es la dirección adecuada de la fuerza, si solo nos imaginamos girando un objeto fijo a una cuerda de longitud fija. La cuerda tiene tensión constante, y es la que "fuerza" al objeto a seguir su movimiento circular. De acuerdo a la experiencia cotidiana, se sabe que el objeto en movimiento jala hacía afuera la mano que sostiene la cuerda. De la tercera
ley de
Newton, se concluye que la fuerza que debe ejercer la mano sobre el objeto, a través de la cuerda, será un tirón hacia adentro igual. Esta fuerza que se dirige hacia el centro, y que gira sobre el objeto, se denomina
fuerza centrípeta y la aceleración que se dirige hacia el centro de giro del objeto se llama
aceleración centrípeta a.
La segunda ley de Newton determina el movimiento circular y los demás movimientos de una partícula. La aceleración, dirigida el centro del circulo, que tiene una partícula con movimiento circular uniforme ha de ser producida por una
fuerza dirigida también hacia el centro. Como la magnitud de la aceleración normal es igual a
v2 / R, y su dirección es hacia su centro, la magnitud de la fuerza normal sobre una partícula de masa
m es
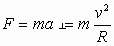
Generalmente hay varias fuerzas que actúan sobre un cuerpo con movimiento circular uniforme. En este caso, el
vector suma de todas las fuerzas que actúan sobre el cuerpo ha de tener la magnitud dada por la ecuación y de estar dirigido directamente hacia el centro del circulo.
La fuerza que aparece en la ecuación se denomina a veces
fuerza centrípeta. El termino no es un afortunado, puesto que parece implicar que esta fuerza es de alguna manera diferente de las demás fuerzas ordinarias, o que el movimiento circular genera de algún modo una fuerza adicional; nada de este es correcto. El termino de centrípeta se refiere al efecto de la fuerza, es decir, al hecho de que ocasionan un movimiento circular en el cual cambia la dirección de la velocidad, pero no su magnitud.
Centrífuga significa <<escapar de un centro>> examinemos esta opinión. En primer lugar, el cuerpo
no permanece en esa posición. Un instante después ocupara una posición distinta sobre su trayectoria circular. En el instante considerado esta moviéndose en la dirección del vector velocidad
v y a menos que actué una fuerza resultante sobre él, continuará moviendo en esta dirección, según la primera ley de Newton. Si estuviera actuando sobre él una fuerza hacia fuera, igual y opuesta a la componente hacia dentro de la fuerza T, no habría fuerza resultada hacia dentro para desviarlo lateralmente de su dirección de movimiento actual.
Cuando se hace girar en círculo una pelota, ésta es acelerada ‘hacia dentro’. La aceleración se debe a una fuerza centrípeta (que tiende hacia el centro): la tensión de la cuerda. La fuerza necesaria es igual a
mv2/
r, donde
m es la masa de la pelota,
v su velocidad y
r el radio de la circunferencia descrita. La mano que tira de la cuerda experimenta una fuerza de reacción centrífuga (dirigida hacia fuera).
El
sistema de rotor de un helicóptero depende principalmente de su rotación para generar la sustentación necesaria para el vuelo. Debido a su rotación
y peso, el rotor esta sujeto a fuerzas
y momentos característicos de todas las masas en rotación. Una de las fuerzas producidas es la
Fuerza Centrífuga. Esta, es definida como la fuerza que tiende a que todos los cuerpos en rotación traten de alejarse de su eje.
Otra de la fuerza que se generan es la
Fuerza Centrípeta. Esta es la fuerza opuesta a la centrífuga, que hace que los componentes de un sistema en rotación traten de acercarse a su eje.
La rotación de las palas de un helicóptero producen una muy alta fuerza centrífuga, cargando la misma sobre el rotor
y el conjunto de las palas. Imaginen que la carga sobre la raíz de la pala puede estar en el orden de las 6 a las 12 toneladas, en un helicóptero de 2 a 4 pasajeros. Helicópteros más grandes pueden experimentar, en cada pala, unas 40 toneladas sobre la raíz.
La fuerza Centrífuga es una de las fuerzas dominantes en el estudio de las alas rotativas.
Cuando las palas del rotor de un helicóptero no están girando, caen hacia abajo debido a su propio peso. Cuando comienza la rotación de¡ conjunto las palas comienzan a elevarse de su posición de descanso debido a la fuerza centrifuga.
A velocidad operacional, debido a su ángulo de ataque, las palas se encuentran en posición "recta", todavía no están generando sustentación.
Cuando el rotor comienza a generar sustentación,.las palas abandonan su posición "recta" y comienzan a generar una posición de "cono". La medida de este cono depende de las RPM, el peso total, y las fuerzas G experimentadas en el vuelo. Si las RPM permanecen constantes, el cono aumenta si, el peso total y las fuerzas G son aumentadas. También, si las RPM disminuyen, manteniendo el peso y las G constantes, el cono va a aumentar.
Excesivo "cono" (coning) causa fatiga sobre las palas además de una disminución de la sustentación al disminuir el área del disco rotor.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Note que el diámetro efectivo del disco del rotor, con el coning incrementando, es menor que el otro disco sin coning. A menor diámetro de disco obtendremos menor sustentación.
La fuerza centrífuga y los efectos de la sustentación pueden ser mejor entendidos con un gráfico. Primero mire un eje de rotor y una pala rotando.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
Ahora observe el mismo rotor cuando una fuerza vertical le es aplicada en la puntera de la pala.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
La fuerza aplicada es la sustentación producida cuando las palas aumentan su ángulo de ataque. La fuerza horizontal es la fuerza centrifuga generada por el rotor al girar. Debido a que la raíz de la pala esta sujeta al árbol, solo el otro extremo tiene la
libertad de moverse y se obtiene una resultante en la pala.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
La posición de la pala es la resultante de dos fuerzas: La sustentación y la fuerza centrífuga.
LEY DE GRAVITACIÓN UNIVERSAL.
Valor de g
Desde la más remota antigüedad,
el hombre ha sentido atraído por el
comportamiento de los astros y ha tratado de buscarle explicación. Así desde la época de los griegos, pasando por Tolomeo y Copérnico con un sistema heliocéntrico se fue evolucionando hasta llegar a la época de Tycho Brahe, el cual hizo mediaciones más precisas de las posiciones de los cuerpos celestes.
Partiendo de los
datos cuidadosamente seleccionados por Brahe, el astrónomo Johanees Kepler enuncio sus famosas
leyes, conocidas hoy como
leyes de kepler. Estas leyes fueron enunciadas así:
Primera Ley:
Todo planeta gira alrededor del sol describiendo una orbita elíptica en la cual
el sol ocupa uno de los focos.
Segunda Ley:
El radio focal que une a un planeta con el sol describe áreas iguales en tiempos iguales.
Tercera Ley:
Para todos los
planetas, la relación entre el cubo del radio de la orbita y el cuadrado de su período es constante, pudiéndose escribir que:
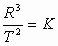
Kepler había pretendido darle explicación a las causas de las leyes que rigen el movimiento de los planetas, pero fue newton quien le dio solución
dinámica al problema del movimiento de los planetas con su ley de Gravitación Universal.
Newton basándose en las leyes de Kepler y en las leyes de la
mecánica, llego a la
deducción de la formula de la Ley de Gravitación Universal.
Deducción de la Ley de Gravitación Universal.
Si se considera que los planetas se mueven en orbitas circulares, la aceleración centrípeta de cualquier planeta se puede calcular por la formula:
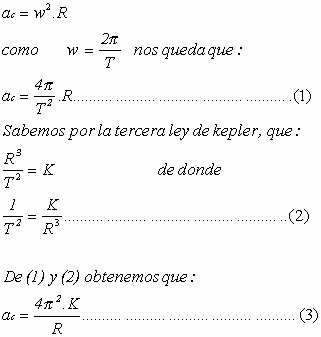
Esto significa que la aceleración de cualquier planeta es independiente de su masa e inversamente proporcional al cuadrado del radio de su orbita.
Por la segunda Ley de Newton la fuerza que le imprime al planeta esta aceleración es:
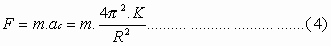
Es decir, la fuerza que actúa sobre cualquier planeta es directamente proporcional a su masa e inversamente proporcional al cuadrado de la distancia de este al sol.
De acuerdo con la tercera ley de Newton, la fuerza con que el sol actúa sobre el planta es de la misma magnitud y de sentido opuesto a la fuerza con que el planeta actúa sobre el sol. Si M es la masa del sol, esta última fuerza puede escribirse como:
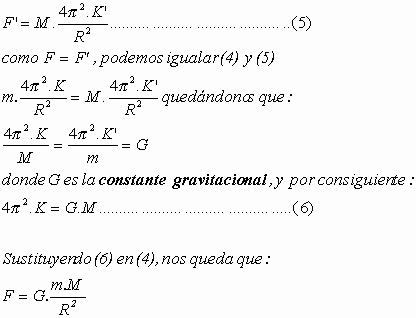
Esta última es la expresión
matemática de la Ley de gravitación universal si se admite la existencia de un campo gravitatorio para todos los cuerpos, la Ley de Newton puede generalizarse para todos los cuerpos del
universo enunciándola así.
"
Dos cuerpos cualesquiera del universo se atraen mutuamente con una fuerza que es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que existe entre sus centros."
Las fuerzas con que se atraen las dos masas no son más que un par de
acción y reacción. La primera masa ejerce una fuerza de atracción sobre la segunda, que esta dirigida hacía la primera, en cambio la segunda masa ejerce otra fuerza de atracción sobre la primera, que esta dirigida hacía la segunda
- F2-1: Fuerza ejercida por M sobre m
- F1-2: Fuerza ejercida por m sobre M.
Para ver el gráfico seleccione la opción "Descargar" del menú superior
El valor de
la constante de gravitación universal G fue determinada por Henry Cavendish, usando una balanza de
torsión, encontrando que:
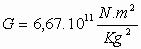 TIPOS DE FUERZAS FUNDAMENTALES
TIPOS DE FUERZAS FUNDAMENTALES
Existen cuatro (4) tipos de fuerzas fundamentales:
Se entiende por
elasticidad a la
propiedad que poseen los cuerpos de recuperar su forma original una vez deformados por el efecto de una fuerza externa. Todos los cuerpos ern mayor o menor grado son elásticos, dependiendo dicha elasticidad de factores tales como la
estructura molecular interna y la fuerza exterior que se aplique.
A las fuerzas de restauración, originadas en la parte interna del material, que tienen a regresar el cuerpo a su posición original y que están aplicadas sobre el cuerpo que origina la deformación se llaman
Fuerzas elásticas.
Si dicho resorte está fijo en un extremo y por el extremo libre ejercemos una fuerza (
acción), aparecerá una reacción que el resorte ejerce sobre nuestra mano con una fuerza dirigida en sentido opuesto a la deformación y su valor depende del alargamiento sufrido por el resorte. Esta fuerza se llama
fuerza Elástica recuperadora.
Cuando un cuerpo esta colocado sobre un plano horizontal, el cuerpo ejerce sobre el plano una fuerza que comprime las moléculas de la superficie del plano en contacto, deformándolo. A su vez, la superficie del plano trata de recuperar su
estado original a través de las fuerzas elásticas, que en este caso se les llama
Fuerzas de contacto normal. La dirección de esta fuerza es perpendicular a las superficies en contacto, razón por la cual se le llama
Normal y se ejerce sobre el objeto causante de la deformación. Denotándose con la letra (N).
La fuerza Normal entre dos superficies en contacto es la fuerza perpendicular que la superficie soporte ejerce sobre la superficie que se encuentra sobre ella.
Es la fuerza ejercida por una cuerda, considerada de masa despreciable e inextensible sobre un cuerpo que esta ligado a ella.
Las fuerzas de fricción y coeficientes de rozamiento.
Son fuerzas que se originan en la superficie de contacto entre dos cuerpos.
Son conocidas dos tipos de fricción: la misma fricción
estática y la fricción cinética.
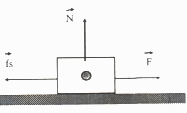
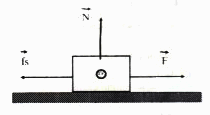
Para comprender mejor estos aspectos donde se
muestra un bloque que esta en reposo sobre un plano horizontal. Al aplicar una fuerza externa F, de dirección horizontal y sentido hacía la derecha, notamos que el bloque no se pone en movimiento. Esto es debido a otra fuerza aplicada y que recibe el nombre de Fuerza de Fricción estática (Fs)
Si aplicamos una fuerza aun mayor que la anterior, y no lo logramos poner el bloque en movimiento, es porque la fuerza equilibradamente de fricción estática también irá aumentado.
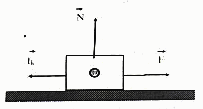
Si se continúa aumentando la fuerza F, llegará un momento en que la fuerza de fricción estática alcance su valor máximo Fs(máx) y el bloque este a punto de ponerse en movimiento.
Al ponerse en movimiento la fuerza de fricción retardadora es menor que la fuerza de fricción retardadora es menor que la fuerza fricción estática máxima. En este caso a la fuerza retardadora se le conoce como fuerza de Fricción Cinética, la cual notaremos fk.
Después de múltiples
experimentos se ha podido comprobar que tanto la magnitud de fs son proporcionales a la magnitud de la fuerza normal N que actúa sobre el bloque.





 es la fuerza que actúa entre los dos cuerpos.
es la fuerza que actúa entre los dos cuerpos. es la distancia entre las dos cargas
es la distancia entre las dos cargas es el vector unitario en la dirección y sentido de
es el vector unitario en la dirección y sentido de 
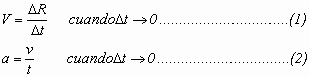
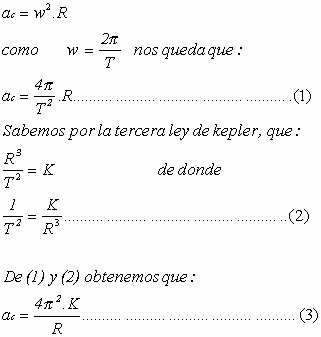
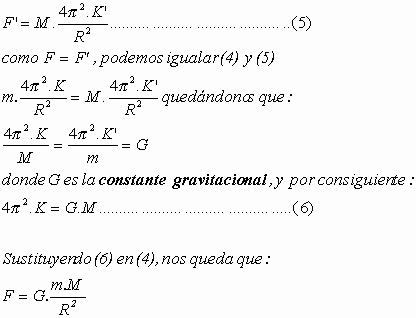









 y
y  , respectivamente, la velocidad relativa de B con respecto a A se denota como
, respectivamente, la velocidad relativa de B con respecto a A se denota como  y viene dada por:
y viene dada por: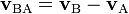
 y viene dada por:
y viene dada por: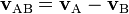

 y
y 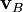 , respectivamente.
, respectivamente.