 y
y  , respectivamente, la velocidad relativa de B con respecto a A se denota como
, respectivamente, la velocidad relativa de B con respecto a A se denota como  y viene dada por:
y viene dada por:Naturalmente, la velocidad relativa de A con respecto a B se denota como
 y viene dada por:
y viene dada por:de modo que las velocidades relativas
 y
y  tienen el mismo módulo pero sentidos opuestos.
tienen el mismo módulo pero sentidos opuestos.El cálculo de velocidades relativas en mecánica clásica es totalmente aditivo y encaja con la intuición común sobre velocidades; de esta propiedad de la aditividad surge el método de la velocidad relativa.
Las definiciones y propiedades anteriores para dos observadores en movimiento relativo se aplica también para el caso de dos partículas clásicas A y B, cuyas velocidades medidas por un observador dado sean
 y
y 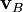 , respectivamente.
, respectivamente.
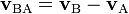
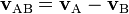

No hay comentarios:
Publicar un comentario